01: Attention is All You Need(Transformer)

Author

Yuyang Zhang

1 Preliminary

在理解Transformer之前，我们需要先了解一些基本的概念。有基础的同学可以跳过这一节，直接看下一节的Transformer模型架构。

1.1 Dot Product Similarity（点积相似度）

给定两个向量 \(\mathbf{q}, \mathbf{k} \in \mathbb{R}^d\), 它们的点积为: \[ \text{score}(\mathbf{q}, \mathbf{k}) = \mathbf{q} \cdot \mathbf{k} = \sum_{i=1}^{d} q_i k_i \tag{1}\] 这个score用于测量两个向量的相似度, 数值越大，说明两个向量越相似

1.2 Softmax 函数

给定向量 \(\mathbf{x} = (x_1, x_2, \ldots, x_n)\)，softmax 函数定义为: \[ \text{softmax}(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}} \tag{2}\] softmax 函数将向量 \(\mathbf{x}\) 转换为一个概率分布，所有元素的和为1。它常用于将模型的输出转换为概率分布。其中，计算softmax 的时间复杂度为 \(\mathcal{O}(n)\)，其中 \(n\) 是向量 \(\mathbf{x}\) 的维度。

1.3 Matrix Multiplication

给定矩阵 \(\mathbf{A} \in \mathbb{R}^{m \times n}\) 和 \(\mathbf{B} \in \mathbb{R}^{n \times p}\)，它们的矩阵乘法定义为: \[ \mathbf{C} = \mathbf{A} \cdot \mathbf{B} \in \mathbb{R}^{m \times p} \tag{3}\] 矩阵乘法是线性代数中的基本运算，用于将两个矩阵相乘，得到一个新的矩阵。它在神经网络中被广泛使用，尤其是在计算注意力分数时。其中，Matrix Multiplication的时间复杂度为 \(\mathcal{O}(mnp)\)，其中 \(m\) 是 \(\mathbf{A}\) 的行数，\(n\) 是 \(\mathbf{A}\) 的列数，也是 \(\mathbf{B}\) 的行数，\(p\) 是 \(\mathbf{B}\) 的列数。 Wikipedia 上有一个关于 Matrix Multiplication Time Complexity 的详细介绍。

2 Attention is All You Need

在这个篇章中，我们将深入阅读这篇论文，首先，我们先来了解一下这篇论文的背景和主要贡献

The dominant sequence transduction models are based on complex recurrent or convolutional neural networks … We propose a new simple network architecture, the Transformer, based solely on attention mechanisms, dispensing with recurrence and convolutions entirely.

本篇论文提出：序列建模（Sequence Modeling）长期依赖 RNN/CNN，其计算受制于时间步骤的串行性，难以并行化，且长距离依赖捕获效率低。为了解决这个问题，作者提出了Transformer模型，完全基于注意力机制，去除了循环和卷积操作，从而实现了全局信息交互。利用多头注意力机制（Multi-Head Attention）+ 前馈网络 （Feed Forward Network）的编码器-解码器，去除了循环/卷积，仅靠注意力实现全局信息交互。 除此之外，他们还设计了Scaled Dot-Product Attention 和 Multi Head Attention，来降低数值尺度的同时并行学习多子空间表示。

以下是Transformer的整体架构图：

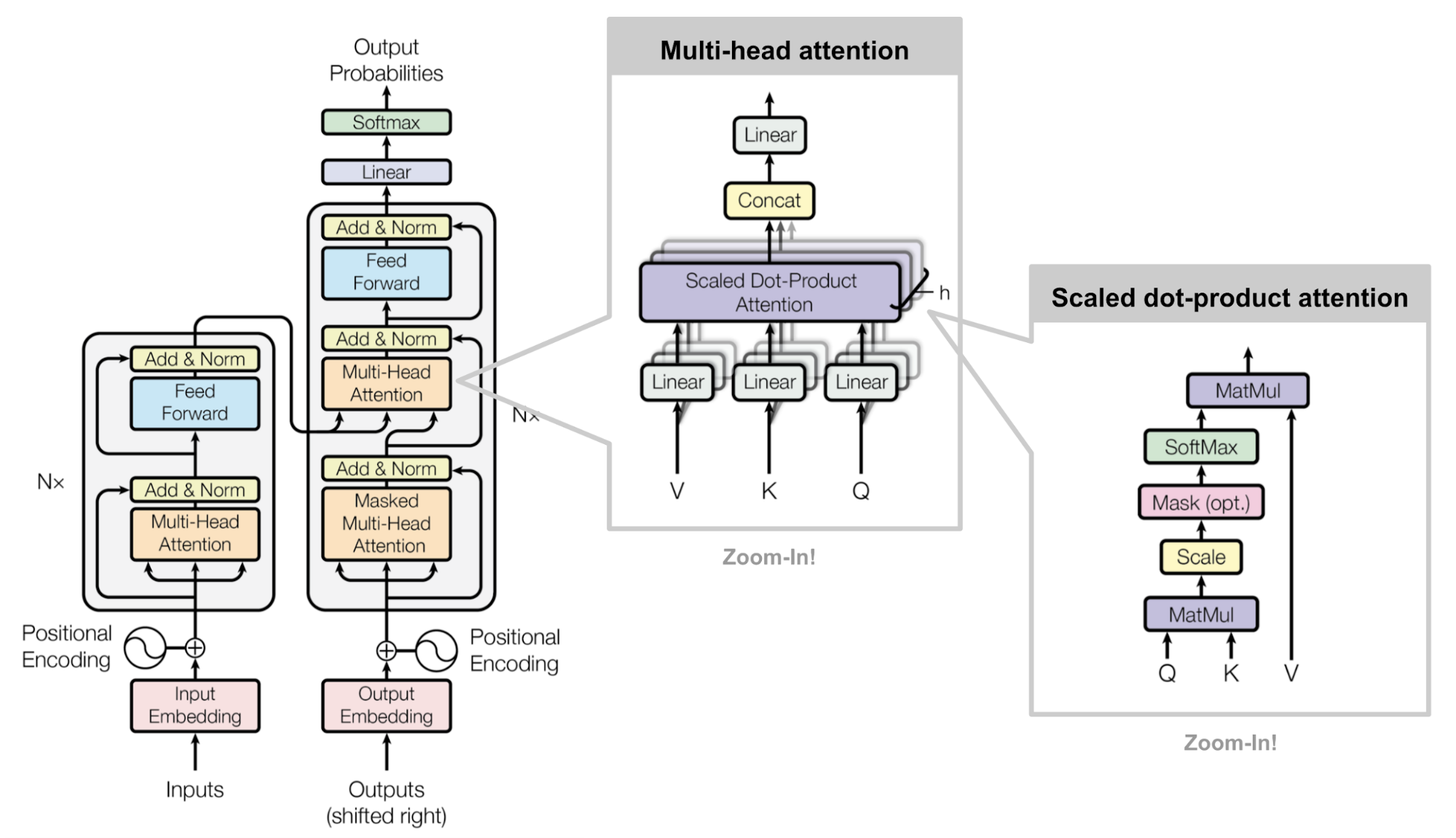
Figure 1: The Transformer Family Version 2.0 | Lil’Log

如图 Figure 1 所示，Transformer是由：

这几个小模块来组成的，每个小模块组成一个Encoder Block，多个Encoder Block堆叠起来形成Encoder，Decoder Block也是类似的。接下来，我们会逐个介绍这些模块。

2.1 Input Embedding

Input Embedding是将输入的token转换为向量的过程。Transformer的输入是一个序列，序列中的每个词都被转换为一个向量。这个向量可以是预训练的词向量，也可以是随机初始化的向量。Transformer使用Word Embedding来将每个token转换为一个固定维度的向量。这在自然语言处理（NLP）中是一个常见的做法。

2.2 Positional Encoding

Transformer 的一个重要特点是它不使用循环神经网络（RNN）或卷积神经网络（CNN）来处理序列数据。这就导致了一个问题：Transformer无法捕捉到序列中词语的位置信息。为了解决这个问题，Transformer引入了位置编码（Position Encoding）。

Since our model contains no recurrence and no convolution, in order for the model to make use of the order of the sequence, we must inject some information about the relative or absolute position of the tokens in the sequence.

位置编码是一个向量，它为每个词提供了一个唯一的位置信息。位置编码的维度与词向量的维度相同。Transformer使用位置编码来为每个词提供一个唯一的位置信息，从而使得模型能够捕捉到词语在序列中的相对位置关系。

在Transformer中，位置编码是通过正弦和余弦函数来实现的：具体来说，对于序列中的第 \(pos\) 个位置，位置编码的第 \(i\) 维可以表示为： \[ \begin{align} \mathrm{PE}(pos,2i)=\sin\!\bigl(pos \times \tfrac{1}{10000^{2i/d_\mathrm{model}}}\bigr) \\ \mathrm{PE}(pos,2i{+}1)=\cos\!\bigl(pos \times \tfrac{1}{10000^{2i/d_\mathrm{model}}}\bigr) \end{align} \tag{4}\]

其中 \(d_{\text{model}}\) 是位置编码的维度（与Word Embedding 的维度一样大）。位置编码的作用是为每个词提供一个唯一的位置信息，使得模型能够捕捉到词语在序列中的相对位置关系。

(a) Position Encoding with max sequence length 100
(b) Position Encoding with max sequence length 100
(c) Position Encoding with max sequence length from 100 to 200
(d) Position Encoding with log base from 10,000 to 1,000
Figure 2: Illustration of Position Encoding with different max sequence lengths, the horizontal red line represent the encoding at position 50. The encoding is consistent across different max sequence lengths, which allows the model to generalize to longer sequences.

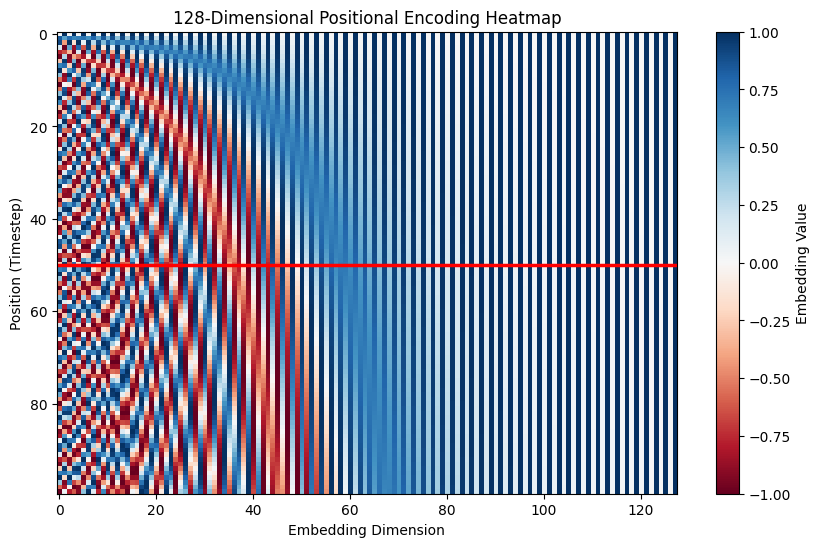
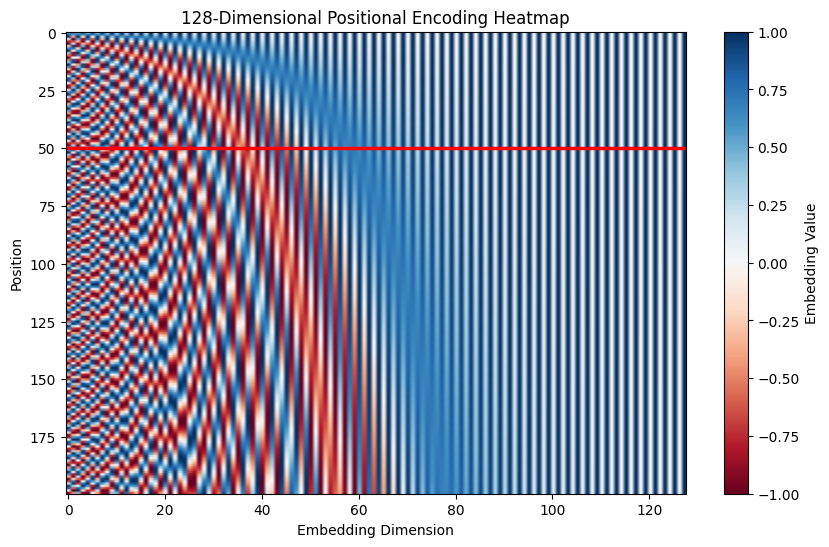
从 Figure 2 中可以看到，随着max sequence length的增加，位置编码的变化是连续的 Figure 2 (c) 。并且在不同的max sequence length下，位置编码的变化是相同的， 图 Figure 2 (a), Figure 2 (b)， 显示的是位置50在不同的max sequence length下的位置编码变化。可以看到，位置编码在不同的max sequence length下是相同的，这使得模型可以更好地泛化到更长的序列上。

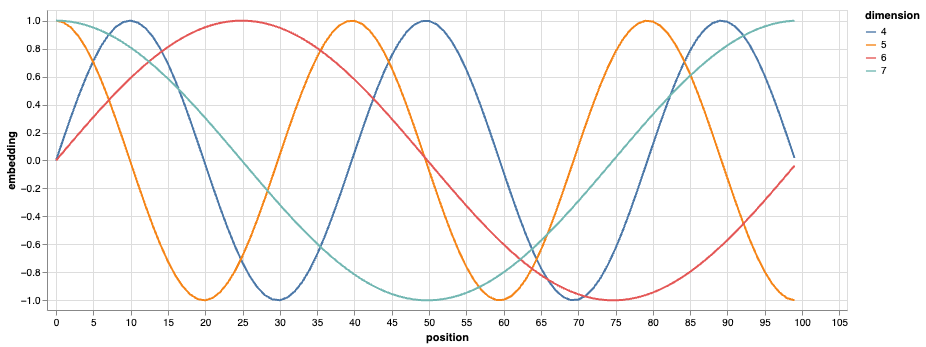
Figure 3: Details of Position Encoding

图 Figure 3 展示了位置编码不同dimension之间的细节。相对于diminution(4, 5), dimension(6,7) 的随着位置变化更大。从图中我们可以看出：

  • 低 \(i\)（靠前的维度）—— 波长短，随位置 pos 变化得快 → 易区别相邻 token；
  • 高 \(i\)（靠后的维度）—— 波长长，随位置 pos 变化得慢 → 捕获全局位置信息。

除此之外，位置编码还可以通过改变正弦和余弦函数的基数来实现不同的效果。比如，可以将基数从10000改为1000，这样可以使得位置编码的波长变短，从而使得模型更容易捕捉到相邻位置的信息。图 Figure 2 (d) 展示了位置编码在不同的基数下的变化。

2.3 Multi-Head Attention

Multi-Head Attention是Transformer的核心模块。它的作用是将输入的向量进行多头注意力计算，从而捕捉到不同的语义信息。Attention 其实就是一个加权求和的过程，它可以看作是对输入向量的加权平均。其核心公式为： \[ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V \tag{5}\]

其中 \(Q\)、\(K\)、\(V\) 分别是查询（Query）、键（Key）和值（Value）矩阵，其中 \(\sqrt{d_k}\) 是一个缩放因子，用来防止点积的值过大导致梯度消失。这个公式的含义是：首先计算查询和键的点积 (Section 1.1) ，然后通过Softmax函数 (Section 1.2) 将其转换为概率分布，最后用这个概率分布对值进行加权求和。

Note

Equation 5 是Attention的核心公式，而Attention是Transformer的核心模块。理解这个公式是理解Transformer的关键。后续很多的创新比如，Linear Attention (Wang et al. 2020)， Multi-head Latent Attention(DeepSeek-AI et al. 2024) 都是在这个公式的基础上进行改进。

Instead of performing a single attention function with dmodel-dimensional keys, values and queries, we found it beneficial to linearly project the queries, keys and values h times with different, learned linear projections to \(d_k\), \(d_k\) and \(d_v\) dimensions, respectively.

Multi-Head Attention 是Attention Equation 5 的一个扩展，它将输入的向量分成多个子空间（head），然后在每个子空间上独立地计算注意力。最后，将所有子空间的输出拼接起来，得到最终的输出。Multi-Head Attention 的公式为： \[ \begin{align*} \text{MultiHead}(Q, K, V) &= \text{Concat}(\text{head}_1, \ldots, \text{head}_h)W^O \\ \text{where}\ \text{head}_i &= \text{Attention}(QW_i^Q, KW_i^K, VW_i^V) \end{align*} \tag{6}\]

其中 \(W_i^Q, W_i^K \in \mathbb{R}^{d_\text{model} \times d_k}, W_i^V \in \mathbb{R}^{d_\text{model} \times d_v}\) 是用于将输入向量投影到子空间的权重矩阵，\(W^O \in \mathbb{R}^{hd_v \times d_\text{model} }\) 是用于将所有子空间的输出拼接起来的权重矩阵。Multi-Head Attention 的作用是通过多个子空间来捕捉不同的语义信息，从而提高模型的表达能力。

Due to the reduced dimension of each head, the total computational cost is similar to that of single-head attention with full dimensionality.

文章中提到，尽管增加了Heads会增加计算量，但由于每个Head的维度较小，并且可以并行计算，从而提高了模型的效率。

2.3.1 Time Complexity of Multi-Head Attention

在继续了解别的component之前，我们先来分析一下Multi-Head Attention的时间复杂度。假设input的长度为 \(n\)，每个head的维度为 \(d_k\)，那么计算 \(QK^T\) 的时间复杂度为 \(\mathcal{O}(n^2 d_k)\) (Equation 3)。

接下来是Softmax的计算，Softmax的时间复杂度为 \(\mathcal{O}(n)\)(Section 1.2)。对于每个score matrix \(QK^T \in \mathbb{R}^{n \times n}\) 的每一行，我们需要计算 softmax，这需要 \(n\) 次计算。因此，Softmax的时间复杂度为 \(\mathcal{O}(n^2)\)。

之后是对于value的加权，计算复杂度也是 \(\mathcal{O}(n^2d)\). 所以总的时间复杂度为：\(\mathcal{O}(n^2d)\), 随着 \(n\) 的增加，计算复杂度会Polynomial 增长。具体的计算复杂度如下表所示： \[ \begin{array}{|l|l|} \hline \textbf{Step} & \textbf{Time Complexity} \\ \hline QK^\top & \mathcal{O}(n^2 d) \\ \text{softmax}(QK^\top) & \mathcal{O}(n^2) \\ \text{attention} \times V & \mathcal{O}(n^2 d) \\ \hline \textbf{Total} & \mathcal{O}(n^2 d) \\ \hline \end{array} \tag{7}\]

2.3.2 Causal Attention

Causal Attention（因果注意力）是Transformer中的一个重要概念，它的作用是防止模型在训练时看到未来的信息，从而保证模型的自回归特性。具体来说，Causal Attention会在计算注意力时，将未来的信息屏蔽掉，从而使得模型只能看到当前和过去的信息。这样可以保证模型在训练时不会看到未来的信息，从而保证模型的自回归特性。 Causal Attention通常作用在Decoder 模块中。

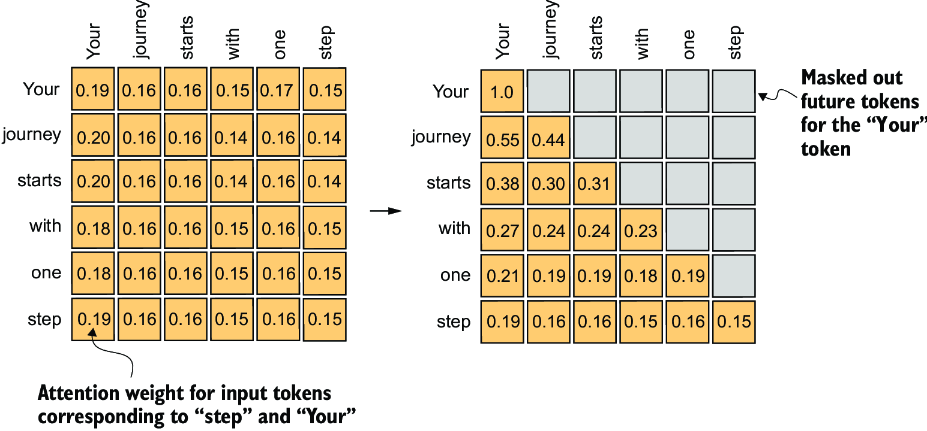
Figure 4: Example of Causal Attention

Causal Attention的公式为： \[ \text{CausalAttention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}} + M\right)V \tag{8}\]

在这个公式中，\(M\) 是一个掩码矩阵（mask matrix），它的作用是将未来的信息屏蔽掉。\(M\) 是一个上三角矩阵，它的对角线以下的元素为0，对角线以上的元素为\(-\infty\)。这样在计算Softmax时，对角线以上的元素会被屏蔽掉，从而保证模型只能看到当前和过去的信息。

2.3.3 Cross Attention

Cross Attention（交叉注意力）作用是将Encoder的输出与Decoder的输入进行交叉注意力计算，从而使得Decoder能够利用Encoder的输出信息。具体来说，Cross Attention会将Encoder的输出作为键（Key）和值（Value），将Decoder的输入作为查询（Query），然后计算注意力。 Cross Attention的公式与Attention Equation 5 类似，只不过将Encoder的输出作为键和值，Decoder的输入作为查询

Note

Cross Attention 除了可以应用在text中，可以应用在不同的modality之间，比如图像和文本之间的交叉注意力。比如在视觉问答（Visual Question Answering）任务中，Cross Attention可以将图像特征与问题文本进行交叉注意力计算，从而使得模型能够利用图像信息来回答问题。

2.4 Layer Normalization

Layer Normalization是Transformer中的一个重要模块，它可以帮助模型更快地收敛。Layer Normalization的作用是对每个位置的向量进行归一化处理，从而使得模型在训练时更加稳定。具体来说，Layer Normalization会对每个位置的向量(feature)进行均值和方差的归一化处理，使得每个位置的向量都具有相同的分布。这样可以使得模型在训练时更加稳定，从而加快模型的收敛速度。

Figure 5: Illustration of Layer Normalization

Layer Normalization的公式为： \[ \text{LayerNorm}(\mathrm{x}) = \frac{\mathrm{x} - \mu}{\sigma + \epsilon} \cdot \gamma + \beta \tag{9}\] 其中 \(\mu\) 是向量 \(\mathrm{x}\) 的均值，\(\sigma\) 是向量 \(\mathrm{x}\) 的标准差。

对于一个batch的输入，Layer Normalization会对每个位置的向量进行归一化处理，而不是对整个batch进行归一化处理。这使得Layer Normalization可以更好地适应不同长度的序列，从而提高模型的性能。具体来说, \(x \in \mathbb{R}^{B \times H \times S \times d_v}\)我们对每个位置的向量也就是 \(d_v\) 维度进行归一化处理，而不是对整个batch进行归一化处理。

2.5 Residual Connection

Residual Connection（残差连接）作用是将输入的向量与子层的输出相加，从而使得模型可以更容易地学习到Identity Mapping。Residual Connection的如图所示：

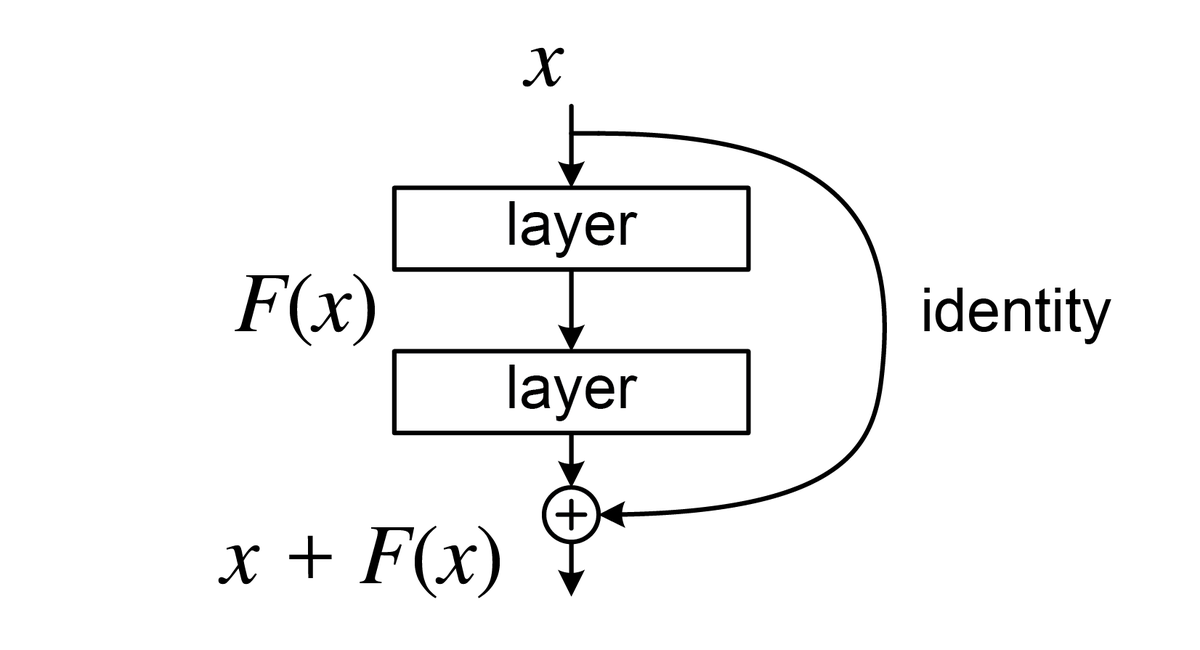
Figure 6: Illustration of Residual Connection

Residual Connection在Transformer的应用公式为： \[ \mathbf{y} = \text{LayerNorm}(\mathbf{x} + \mathrm{Sublayer}(\mathbf{x})) \tag{10}\]

在训练时，残差连接可以为梯度提供一条“捷径”，即梯度可以不经过子层复杂的非线性变换，直接传回前面层的输入。这能有效缓解梯度消失问题。

\[ \begin{align} \frac{\partial \mathcal{L}}{\partial \mathbf{x}} &= \frac{\partial \mathcal{L}}{\partial \mathbf{y}} \cdot \frac{\partial \mathbf{y}}{\partial \mathbf{x}} \\ &= \frac{\partial \mathcal{L}}{\partial \mathbf{y}} \cdot \left( \mathbf{I} + \frac{\partial \mathrm{Sublayer}(\mathbf{x})}{\partial \mathbf{x}} \right) \\ &= \underbrace{\frac{\partial \mathcal{L}}{\partial \mathbf{y}}}_{\text{straight path}} + \underbrace{\frac{\partial \mathcal{L}}{\partial \mathbf{y}} \cdot \frac{\partial\,\mathrm{Sublayer}(\mathbf{x})}{\partial \mathbf{x}}}_{\text{through the sub-layer}} \end{align} \tag{11}\] 其中， \(\mathcal{L}\) 是损失函数。我们可以看到由于存在第一项，哪怕子层梯度接近 0，Gradient 的信息也不会完全丢失。

Pre-Normalization vs Post-Normalization

Transformer论文中, Normalization的位置是放在Residual Connection的后面（Post-Normalization）Equation 10 。但在后续的研究中，很多模型（比如BERT）将Normalization放在Residual Connection的前面（Pre-Normalization）。 \[ \text{Output} = \mathrm{Sublayer}(\mathbf{x}) + \mathrm{LayerNorm}(\mathbf{x}) \tag{12}\]

2.6 Point-Wise Feed Forward Network

In addition to attention sub-layers, each of the layers in our encoder and decoder contains a fully connected feed-forward network, which is applied to each position separately and identically.

Point-Wise Feed Forward Network作用是对每个位置的向量进行非线性变换, 其公式为： \[ \text{FFN}(x) = \max(0, xW_1 + b_1)W_2 + b_2 \tag{13}\]

其中 \(W_1\) 和 \(W_2\) 是线性变换的权重矩阵，\(b_1\) 和 \(b_2\) 是偏置项。Point-Wise Feed Forward Network的作用是对每个位置的向量进行非线性变换，从而使得模型可以更好地捕捉到输入序列中的不同语义信息。

2.7 Output Linear Projection & Softmax

在Transformer的Decoder中，最后一步是将Decoder的输出通过一个线性变换和Softmax函数转换为词汇表中的概率分布。这个过程可以看作是将Decoder的输出映射到词汇表中的每个词的概率。具体来说， \[\text{Output} = \text{Softmax}(xW + b) \tag{14}\] 其中 \(W \in \mathbb{R} ^ {d_\text{model} \times vocab}\) 是线性变换的权重矩阵，\(b\) 是偏置项。Softmax函数将线性变换的输出转换为概率分布，从而使得模型可以生成下一个词的概率分布。

在这个过程中，Transformer 的作者采用了一种 weight tying(Press and Wolf 2017) 的方法，将输入的词嵌入矩阵和输出的线性变换矩阵共享同一个权重矩阵。这种方法可以减少模型的参数量，从而提高模型的效率，并且在实践中效果也很好。具体来说，Transformer 的作者将输入的词嵌入矩阵和输出的线性变换矩阵共享同一个权重矩阵，这样可以减少模型的参数量，从而提高模型的效率。

2.8 Full Model

Transformer的完整模型架构如图 Figure 1 所示。Transformer由多个Encoder Block和Decoder Block组成，每个Encoder Block和Decoder Block都包含了前面介绍的模块。Encoder Block和Decoder Block的结构是相似的，都是由Multi-Head Attention、Point-Wise Feed Forward Network、Layer Normalization和Residual Connection组成的。

下图是整个Transformer的编码和解码过程的示意图：

(a) Transformer Encoding Process
(b) Transformer Decoding Process
Figure 7: Illustrate of Transformer Encoding and Decoding Process (Image Source: The Illustrated Transformer)

如图 Figure 7 所示，Transformer的编码过程和解码过程是相似的。编码过程将输入的token转换为向量，然后通过多个Encoder Block进行编码，最后通过一个线性变换和Softmax函数转换为词汇表中的概率分布。解码过程则是将Encoder的输出与Decoder的输入进行交叉注意力计算，然后通过多个Decoder Block进行解码，最后通过一个线性变换和Softmax函数转换为词汇表中的概率分布。

2.9 Training Process

接下来，我们探讨一下Transformer的训练过程。Transformer的训练过程与其他神经网络模型类似，主要包括以下几个步骤：

  1. 数据预处理：将输入的文本数据转换为token，并进行分词和编码。通常使用Word Embedding将每个token转换为一个固定维度的向量。
  2. 模型初始化：初始化Transformer模型的参数，包括Word Embedding、Position Embedding、Multi-Head Attention、Point-Wise Feed Forward Network等模块的参数。
  3. 前向传播：将输入的token通过Word Embedding和Position Embedding转换为向量，然后通过多个Encoder Block进行编码，最后通过一个线性变换和Softmax函数转换为词汇表中的概率分布。
  4. 计算损失：使用交叉熵损失函数（Cross-Entropy Loss）计算模型的输出与真实标签之间的差异。交叉熵损失函数是一个常用的分类损失函数，它可以衡量模型的输出概率分布与真实标签之间的差异。
  5. 反向传播：通过计算损失函数对模型参数的梯度，使用梯度下降算法（如Adam优化器）更新模型的参数。梯度下降算法是一种常用的优化算法，它可以通过计算损失函数对模型参数的梯度来更新模型的参数，从而使得模型的输出更接近真实标签

具体的实现过程，我们将在接下来的PyTorch实现中详细介绍。包括Label Smoothing、Adam、Masking等细节处理。

3 PyTorch 实现

接下来，我们利用PyTorch来实现Transformer的模型架构。我们采用Bottom-Up的方法，先实现Word Embedding， 是Position Embedding，然后实现我们的重点，即Multi-Head-Attention，再次之后，我们会实现 Point-Wise Feed Forward Network。最后将这几个模块组合起来，实现Transformer的Encoder 和 Decoder。准备好了吗？让我们开始吧！

3.1 Word Embedding

Word Embedding是将词语转换为向量的过程。在PyTorch 中的实现非常简单，我们可以使用nn.Embedding类来实现。这个类会将每个token映射到一个固定维度的向量空间中。

class WordEmbedding(nn.Module):
    def __init__(self, config: ModelConfig, is_tgt: bool = False):
        super().__init__()

        if is_tgt:
            self.embedding = nn.Embedding(config.tgt_vocab_size, config.d_model)
        else:
            self.embedding = nn.Embedding(config.src_vocab_size, config.d_model)

    def forward(self, x):
        """
        x: (batch_size, seq_len)
        """
        return self.embedding(x)

3.2 Position Embedding

接下来，我们来实现Position Embedding Equation 4。

class PositionalEmbedding(nn.Module):
    def __init__(self, config: ModelConfig):
        super().__init__()

        pos_index = torch.arange(config.max_seq).unsqueeze(1)  # (max_seq, 1)

        div_term = torch.exp(
            torch.arange(0, config.d_model, 2) * -(math.log(10000.0) / config.d_model)
        )

        pe = torch.zeros(config.max_seq, config.d_model)  # (max_seq, d_model)
        pe[:, 0::2] = torch.sin(pos_index * div_term)
        pe[:, 1::2] = torch.cos(pos_index * div_term)

        pe = pe.unsqueeze(0)  # (1, max_seq, d_model)

        pe.requires_grad = False
        self.register_buffer("pe", pe)

    def forward(self, x):
        """
        x: (batch_size, seq_len, d_model)
        """
        seq_len = x.size(1)
        return self.pe[:, :seq_len, :]  # (1, seq_len, d_model)

有了Word Embedding 和 Position Embedding，我们就可以将输入的token转换为向量了。我们需要接下来需要做的就是，将这两个向量相加，得到最终的输入向量。

class Embedding(nn.Module):
    def __init__(self, config: ModelConfig, is_tgt: bool = False):
        super().__init__()
        self.word_embedding = WordEmbedding(config, is_tgt)
        self.positional_embedding = PositionalEmbedding(config)

    def forward(self, x):
        """
        x: (batch_size, seq_len)
        """
        word_emb = self.word_embedding(x)
        pos_emb = self.positional_embedding(word_emb)
        return word_emb + pos_emb  # (batch_size, seq_len, d_model)

3.3 Feed Forward Network

我们先跳过Multi Head Attention，先实现Feed Forward Network。Feed Forward Network是Transformer中的一个重要模块，它的作用是对每个位置的向量进行非线性变换。具体来说，Feed Forward Network由两个线性变换和一个ReLU激活函数组成。

class FFN(nn.Module):
    def __init__(self, config: ModelConfig):
        super().__init__()

        self.ln1 = nn.Linear(config.d_model, config.d_ff, bias=True)
        self.ln2 = nn.Linear(config.d_ff, config.d_model, bias=True)

    def forward(self, x):
        x = F.relu(self.ln1(x))  # Apply ReLU activation
        x = self.ln2(x)  # Linear transformation
        return x  # (batch_size, seq_len, d_model)

3.4 Layer Normalization

还有一个重要的模块是Layer Normalization，它可以帮助模型更快地收敛。

class LayerNormalization(nn.Module):
    def __init__(self, config: ModelConfig):
        super().__init__()

        self.eps = config.eps

        self.gamma = nn.Parameter(torch.ones(config.d_model))  # (d_model,)
        self.beta = nn.Parameter(torch.zeros(config.d_model))  # (d_model,)

    def _compute_mean_std(self, x):
        """
        Compute mean and standard deviation for the input tensor x
        On the last dimension (features)
        x: (batch_size, seq_len, d_model)
        Output:
            mean: (batch_size, seq_len, 1)
            std: (batch_size, seq_len, 1)
        """
        mean = x.mean(dim=-1, keepdim=True)
        std = x.std(dim=-1, keepdim=True)
        return mean, std

    def forward(self, x):
        mean, std = self._compute_mean_std(x)

        # normalize x: (batch_size, seq_len, d_model)
        normalized_x = (x - mean) / (std + self.eps)  # Avoid division by zero

        return normalized_x * self.gamma + self.beta  # (batch_size, seq_len, d_model)

3.5 Multi Head Attention

Multi Head Attention是Transformer的核心模块。它的作用是将输入的向量进行多头注意力计算，从而捕捉到不同的语义信息。

Important

这部分是Transformer的核心模块，理解它是理解Transformer以及他变型的关键。记得多看几遍，直到你能理解为止。

def scaled_dot_product_attention(q, k, v, mask=None):
    """
    Scaled Dot-Product Attention
    q: (batch_size, num_heads, seq_len_q, d_k)
    k: (batch_size, num_heads, seq_len_k, d_k)
    v: (batch_size, num_heads, seq_len_v, d_v)
    mask: (batch_size, 1, seq_len_q, seq_len_k) or None
    """
    d_k = k.shape[-1]

    scores = einops.einsum(
        q,
        k,
        "batch heads seq_len_q d_k, batch heads seq_len_k d_k -> batch heads seq_len_q seq_len_k",
    )

    scores = scores / math.sqrt(d_k)  # Scale the scores
    scores = F.softmax(scores, dim=-1)  # Apply softmax to get attention weights

    if mask is not None:
        scores = scores.masked_fill(mask, float("-inf"))  # Apply mask if provided

    output = einops.einsum(
        scores,
        v,
        "batch heads seq_len_q seq_len_k, batch heads seq_len_k d_v -> batch heads seq_len_q d_v",
    )

    return output
class MultiHeadAttention(nn.Module):
    def __init__(self, config: ModelConfig):
        super().__init__()

        assert (
            config.d_model % config.num_heads == 0
        ), "d_model must be divisible by num_heads"
        self.d_k = config.d_model // config.num_heads  # Dimension of each head
        self.num_heads = config.num_heads

        self.qkv_proj = nn.Linear(
            config.d_model, config.d_model * 3, bias=True
        )  # (d_model, d_model * 3)

        self.out_proj = nn.Linear(config.d_model, config.d_model, bias=True)

    def forward(self, x, mask=None):
        """
        x: (batch_size, seq_len, d_model)
        mask: (batch_size, 1, seq_len_q, seq_len_k) or None
        """
        batch_size, seq_len, _ = x.size()

        q, k, v = map(
            lambda t: einops.rearrange(
                t,
                "batch seq_len (heads d_k) -> batch heads seq_len d_k",
                heads=self.num_heads,
            ),
            self.qkv_proj(x).chunk(3, dim=-1),
        )  # (batch, num_heads, seq_len, d_k)

        # Compute attention
        attn_output = scaled_dot_product_attention(q, k, v, mask)

        # Rearrange back to (batch_size, seq_len, d_model)
        attn_output = einops.rearrange(
            attn_output,
            "batch heads seq_len d_v -> batch seq_len (heads d_v)",
            heads=self.num_heads,
        )

        output = self.out_proj(attn_output)  # (batch_size, seq_len, d_model)
        return output  # (batch_size, seq_len, d_model)

3.6 Encoder Block

Encoder Block是Transformer的一个重要模块，它由Multi Head Attention和Feed Forward Network组成。它的作用是对输入的向量进行编码，从而捕捉到不同的语义信息。

class EncoderBlock(nn.Module):
    def __init__(self, config):
        super().__init__()

        self.attention = MultiHeadAttention(config)
        self.ffn = FeedForwardNetwork(config)
        self.norm1 = LayerNormalization(config.d_model)
        self.norm2 = LayerNormalization(config.d_model)
        self.dropout = nn.Dropout(config.dropout)

    def forward(self, x):
        # Multi Head Attention
        attn_output = self.attention(x)
        x = self.norm1(x + self.dropout(attn_output))   
        # Feed Forward Network
        ffn_output = self.ffn(x)
        x = self.norm2(x + self.dropout(ffn_output))
        return x

3.7 Decoder Block

Decoder Block是Transformer的另一个重要模块，它与Encoder Block类似，但它还需要处理 Masked Multi Head Attention。Masked Multi Head Attention的作用是防止模型在训练时看到未来的信息，从而保证模型的自回归特性。

class DecoderBlock(nn.Module):
    def __init__(self, config):
        super().__init__()      

        self.attention1 = MultiHeadAttention(config)
        self.attention2 = MultiHeadAttention(config, is_causal=True)

恭喜你，以及成功的实现了Transformer，这个是当前最重要的AI模型框架。理解了它，你就理解可以理解大部分的AI模型了。现在大火的ChatGPT，DeepSeek等模型都是基于Transformer的变型（在接下来的文章中，我们会阅读到这些模型）。完整的代码可以在GitHub上查看。

4 扩展

自从Transformer被提出以来，已经有了很多的变型和改进。具体的来说，Attention在Transformer中需要 \(\mathcal{O}(n^2)\) 的计算复杂度，这在处理长文本时会变得非常慢。因此，很多研究者提出了各种各样的改进方法来降低计算复杂度。以下是一些常见的改进方法：

  • Sparse Attention: 通过稀疏化注意力矩阵来降低计算复杂度。比如，Reformer模型使用了局部敏感哈希（LSH）来实现稀疏注意力。
  • Linear Attention: 通过将注意力计算转换为线性时间复杂度

5 Q&A

回答：如果不缩放，当 \(d_k\) 很大时，QK 的方差也会变大，使 softmax 落入梯度非常小的区域。除以 \(\sqrt{d_k}\) 有助于将激活值保持在适合训练的范围内。

回答：它让模型可以同时关注不同的表示子空间和位置的信息，从而克服单头自注意力容易“平均化”的问题。

回答：解码器通过将未来位置的注意力得分设为 \(-\infty\) 来屏蔽它们，确保每个位置只能关注到前面的输出。

回答：正弦位置编码允许模型推广到更长的序列，参数量少，并且在 BLEU 分数上与可学习的位置编码效果相当。

回答：自注意力的路径长度是常数，每层的计算复杂度是 \(\mathcal{O}(n²d)\)；而 RNN 需要 \(\mathcal{O}(n)\) 的串行步骤，CNN 需要堆叠多层才能覆盖长距离依赖。

References

DeepSeek-AI, Aixin Liu, Bei Feng, Bin Wang, Bingxuan Wang, Bo Liu, Chenggang Zhao, et al. 2024. “DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model.” June 19, 2024. https://doi.org/10.48550/arXiv.2405.04434.
Press, Ofir, and Lior Wolf. 2017. “Using the Output Embedding to Improve Language Models.” February 21, 2017. https://doi.org/10.48550/arXiv.1608.05859.
Wang, Sinong, Belinda Z. Li, Madian Khabsa, Han Fang, and Hao Ma. 2020. “Linformer: Self-Attention with Linear Complexity.” June 14, 2020. https://doi.org/10.48550/arXiv.2006.04768.